Dit is het derde en laatste stukje over de Masters’ Correctiefactoren. Ik kijk hierin alleen naar de resultaten van Masters, waardoor deze resultaten iets afwijken van de vorige stukjes, waarin ook senioren werden meegenomen. Maar het idee is dezelfde: om juiste correctiefactoren te berekenen moet je een realistisch model van bootsnelheid gebruiken. Een noodzakelijke tussenstap daarin is vermogen, want in één stap van leeftijd naar snelheid werkt niet. Zo kan het verband tussen leeftijd, vermogen en bootsnelheid tot uitdrukking komen. En ik beperk me tot de recordhouders en kijk niet, zoals Breda, naar de top 10%.

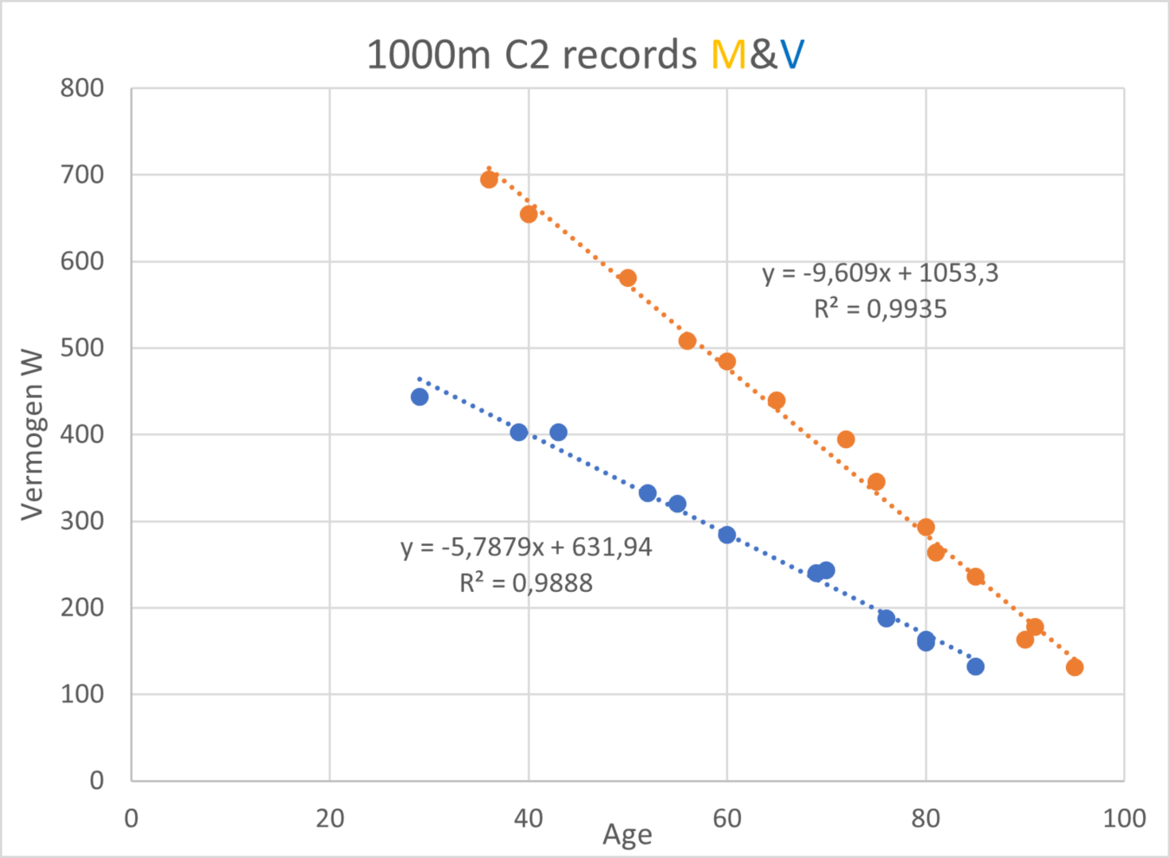
Ik vat even samen wat het ‘1K lineair vermogensverlies’ opleverde.  Het grafiekje hieronder toont het 1000m Concept2 record vermogen van de recordhouders in de leeftijd van 30 tot 90,. De lineaire relatie is wel duidelijk. De correlaties zijn haast perfect met R²  bijna gelijk 1.

Volgende stap gaat van record-vermogen naar recordsnelheid. Ik heb alle resultaten van de laatste 3 World masters en de laatste Euromasters doorplozen en alle 1K-recordtijden voor alle boten, M en V, en leeftijdsklassen verzameld. Niet met de werkelijke leeftijd van de winnaars, da’s teveel gepuzzel, maar de laagste categorie-leeftijd + 1 jaar. Die recordtijden tegen het bij die leeftijd behorende recordvermogen heb ik in een dubbel-logaritmische grafiek gezet en daar de correlatie van bepaald.

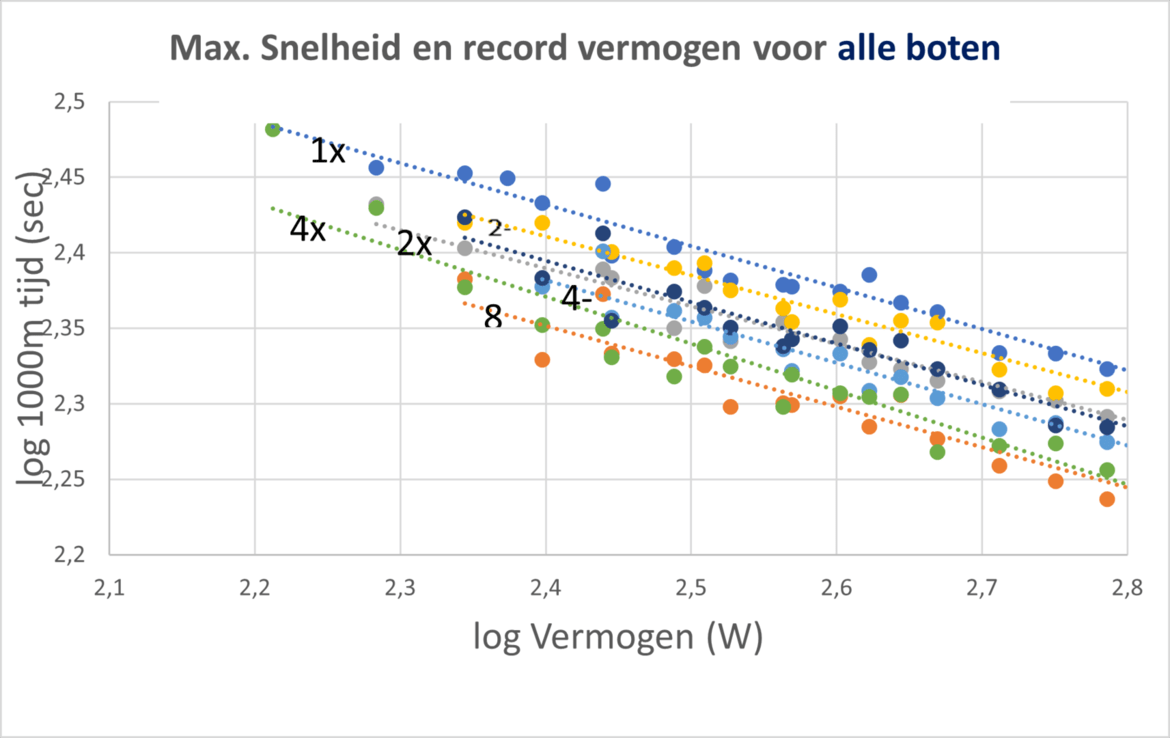De lineaire trendlijnen benaderen dus de ‘recordlijnen’ voor alle boten. Met deze recordlijnen en de vermogen/leeftijdsrelaties kunnen dus formules voor recordtijd per leeftijd en geslacht worden afgeleid. Die formules zien er zo uit: log(recordtijd) = D + A*log(B + C*leeftijd)

A, B, C en D zijn constanten die kunnen verschillen naar boot, geslacht en afstand. Voor de 1000 m zijn B en C resp. 1053,3 en 9,609 voor mannen en 631,94 en 5,7879 voor vrouwen. A en D zijn bootafhankelijk: 

De correlaties waren niet allemaal even goed. Met name de grotere nummers 8 en 4 hadden een lagere R²; skiff en tweeën waren beter. Met deze waarden kunnen de correctiefactoren berekend worden door te normaliseren met de tijd van de 30 jarige skiffeur. 

Deze leeftijds-correctiefactoren wijken sterk af van die van Breda: zie grafiek hieronder. De belangrijkste reden lijkt dat de Breda-factor sterk wordt beïnvloed door groter vermogensverlies van veel ouderen: in de C2-vermogenscorrectie gebeurd dat niet. Ook is de vrouw-factor niet 0,9 en ook niet constant: 0.86-0.88.

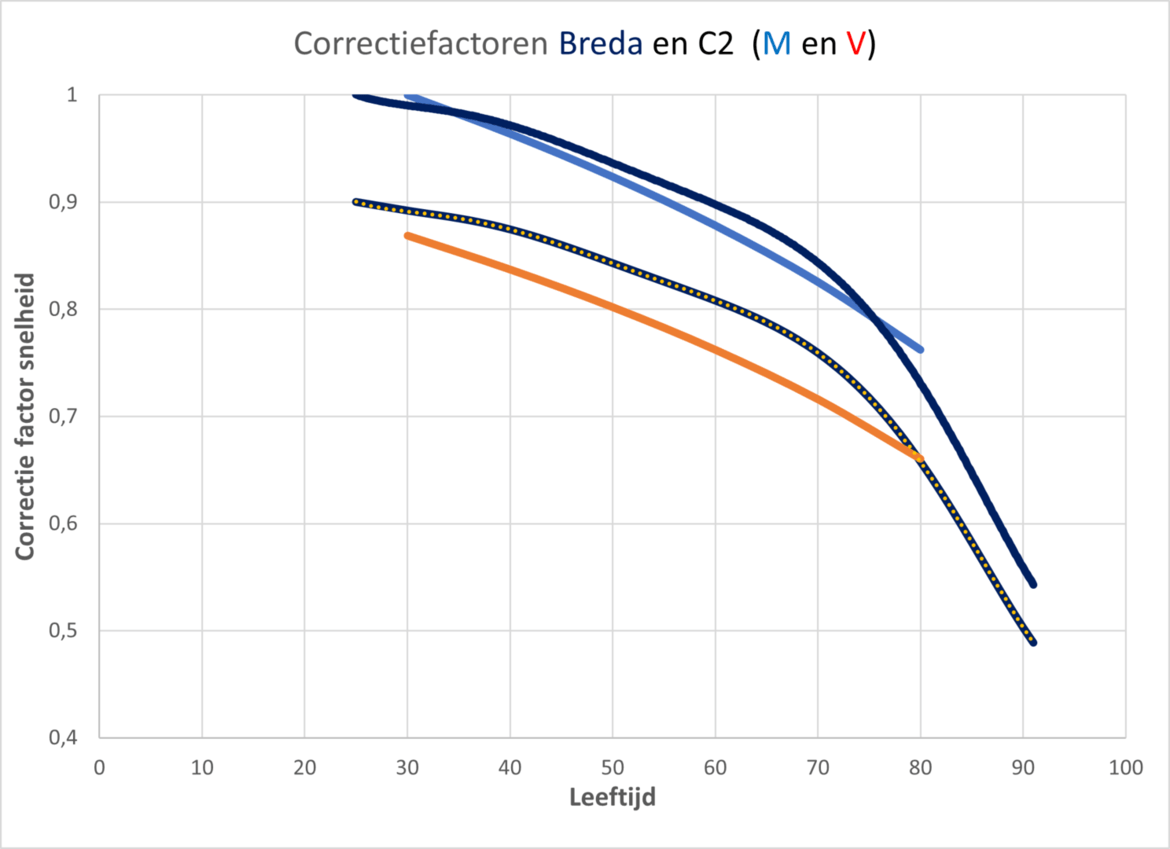
De bootfactoren tenslotte zijn iets leeftijdsafhankelijk maar niet veel. Ook wijken enkele af van die van Breda: 

Dit geldt allemaal voor 1K. Voor andere afstanden e.g. 2K, 4K, 8K zijn aparte berekeningen nodig en een dataset van representatieve baanrecords. Het vermogensverlies met leeftijd voor grotere afstanden dan 1K is bijvoorbeeld niet langer 1^e graads (lineair) maar 2^e graads. Dat geeft andere correcties, zoals ik heb laten zien in het grafiekje over de Silverskiff.

Henk Helle